Messungen sind unverzichtbar für die Qualitätssicherung in der Fertigung. Doch jedes Messergebnis ist mit Unsicherheit behaftet. Der folgende Beitrag erläutert zentrale Begriffe der Messtechnik und zeigt anhand eines Beispiels, wie sich Messunsicherheiten systematisch bestimmen und bewerten lassen.

Die Messtechnik, also die Wissenschaft und Anwendung von Messungen, ist ein wertschöpfender Prozess in Fertigungsumgebungen. Mithilfe geometrischer Messsysteme, wie beispielsweise Koordinatenmessgeräten und strukturierten Lichtscannern, bestimmen wir, ob die Abmessungen von Bauteilen den Konstruktionstoleranzen entsprechen. In ähnlicher Weise verwenden wir optische und Tast-Oberflächenmess­systeme, um zu überprüfen, ob die Oberflächenrauheit den Konstruktionsanforderungen für die Montage und Funktion entspricht. Obwohl diese Instrumente genaue Ergebnisse liefern können, ist ein Messergebnis immer mit einer gewissen Unsicherheit behaftet. Wie im ISO-Leitfaden zur Angabe der Unsicherheit bei Messungen festgelegt, sind wir verpflichtet, nicht nur das Messergebnis, sondern auch eine „quantitative Angabe der Qualität des Ergebnisses“ oder Unsicherheit anzugeben [1].

Ein guter Ausgangspunkt für die Umsetzung dieser Leitlinien ist eine Überprüfung der gängigen Begriffe und Definitionen der Messtechnik [2]:

• Die Genauigkeit (einer Messung) ist die Übereinstimmung zwischen dem Ergebnis einer Messung und dem (wahren) Wert. Es ist wichtig zu beachten, dass Genauigkeit ein qualitativer Begriff ist. Mit anderen Worten, Zahlen sollten nicht damit in Verbindung gebracht werden.
   
• Der Fehler (einer Messung) ist das Ergebnis einer Messung abzüglich des (wahren) Wertes. Da der wahre Wert nicht bestimmt werden kann, wird in der Praxis manchmal ein „konventioneller wahrer Wert“ verwendet.
   
• Die Unsicherheit (einer Messung) ist ein Parameter, der die Streuung der Werte charakterisiert, die dem Messergebnis vernünftigerweise zugeordnet werden können. Die Unsicherheit kann mit statistischen Methoden oder aus angenommenen Wahrscheinlichkeitsverteilungen auf der Grundlage von Erfahrungen oder anderen Informationen quantifiziert werden.
   
• Die Auflösung ist die kleinste erkennbare Größe.
   
• Die Wiederholbarkeit (von Messergebnissen) ist die Übereinstimmung zwischen den Ergebnissen aufeinanderfolgender Messungen desselben Parameters unter denselben Messbedingungen (d.h. gleichem Verfahren, Bediener, Instrument und Ort über einen kurzen Zeitraum). Präzision hat dieselbe Bedeutung wie Wiederholbarkeit; sie sollte nicht synonym mit Genauigkeit verwendet werden.
   
• Reproduzierbarkeit (von Messergebnissen) ist die Übereinstimmung zwischen den Ergebnissen von Messungen desselben Parameters, die unter veränderten Messbedingungen, z.B. durch einen neuen Bediener, durchgeführt wurden.

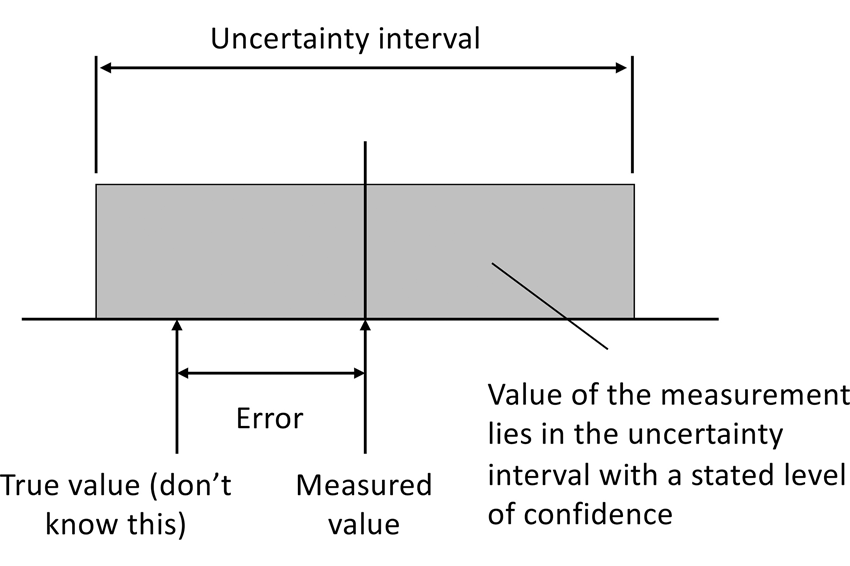
Die Beziehungen zwischen dem gemessenen Wert, dem wahren Wert, dem Fehler und der Unsicherheit werden grafisch dargestellt (siehe Bild 1). Es ist ersichtlich, dass der Wert der Messung mit einem angegebenen Konfidenzniveau innerhalb des Unsicherheitsintervalls liegt. Wenn wir die Messunsicherheit beschreiben, schätzen wir die Standardabweichung, die wir von dieser Messung erwarten würden, wenn sie mit dem ausgewählten Messgerät unter den angegebenen Bedingungen durchgeführt würde.

Mithilfe der Statistik kann die erwartete Streuung für n Messungen einer Größe x charakterisiert werden. Die Beziehungen zwischen den Stichproben xi, dem Mittelwert µ und der Verteilung in den Stichproben werden wiederum grafisch dargestellt (siehe Bild 2). Es zeigt sich eine Normalverteilung. Die Gleichungen für den Mittelwert, die Varianz und die Standardabweichung werden ebenfalls angegeben.

Messungen mit mehreren Variablen: Dichte eines Aluminiumblocks

Einige Messungen basieren auf mehreren Eingaben. In diesem Fall möchten wir die kombinierten Auswirkungen der einzelnen Eingaben auf die Unsicherheit des Mess­ergebnisses bestimmen. Nehmen wir beispielsweise an, wir möchten die Dichte r eines Aluminiumblocks bestimmen. Dazu benötigen wir sowohl die Masse m als auch das Volumen V des Blocks. Wenn wir das Volumen aus den Messungen der drei Seitenlängen L1, L2 und L3 berechnen, erhalten wir vier Eingaben für die Dichteberechnung.

Die kombinierte Standardunsicherheit der Dichte, uc(r), hängt von der Unsicherheit der Massenmessung und den drei Längenmessungen ab. Sie wird mithilfe einer Taylor-Reihe erster Ordnung der Dichtegleichung bestimmt. 

Die kombinierte Standardunsicherheit

Die Gleichung für die kombinierte Standardunsicherheit setzt sich aus vier separaten Termen zusammen, wobei jeder Term das Produkt aus dem Quadrat der partiellen Ableitung (Empfindlichkeit) und dem Quadrat der Messunsicherheit (oder Varianz) für jede Eingabe ist. Die partiellen Ableitungen werden aus den Mittelwerten der Eingaben berechnet. Die Messunsicherheiten für die Eingaben können aus der Standardabweichung wiederholter Messungen (Bewertungstyp A) bestimmt werden oder auf anderen Informationen basieren, zum Beispiel einem vom Hersteller angegebenen Wert (Bewertungstyp B).

Die vier einzelnen Terme können verglichen werden, um zu bestimmen, welcher Eingang den größten Einfluss auf die kombinierte Standardunsicherheit hat. Ist die kombinierte Standardunsicherheit größer als gewünscht, kann anhand des größten Terms ermittelt werden, wo in verbesserte Messgeräte investiert werden sollte. Im Beispiel zur Dichte wäre es sinnvoll, eine Waage mit geringerer Messunsicherheit anzuschaffen, wenn der erste Term in der kombinierten Standardunsicherheitsgleichung der größte ist.

Literatur
IS, C.I. and AS, M., 1993. Guide to the Expression of Uncertainty in Measurement. The International Organization for Standardization ISO.
Taylor, B.N and Kuyatt, C.E., 1994. Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results

Autor
Tony Schmitz, Professor der Universität von Tennessee